Le théorème de Besicovitch

Extrait du livre
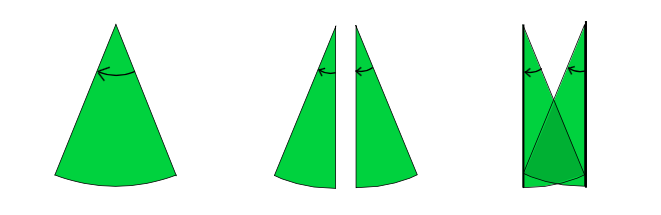
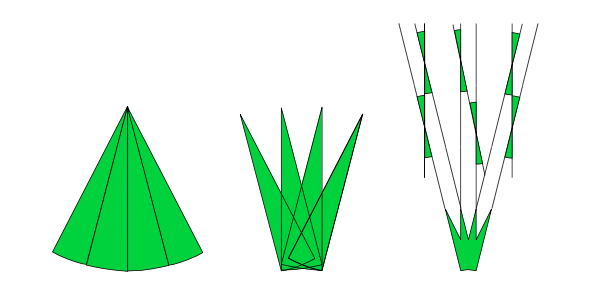
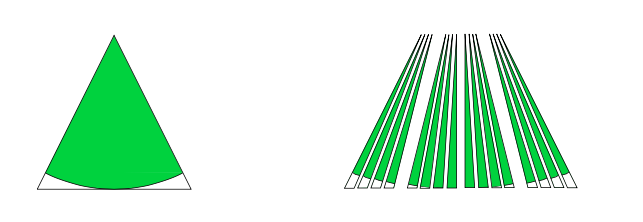
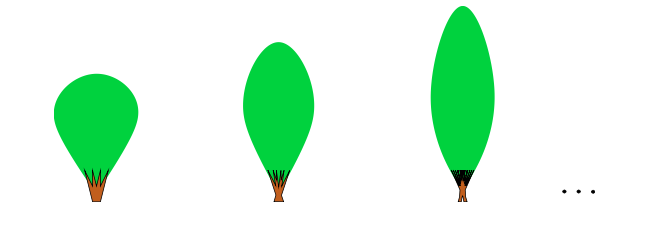
L’illustration ci-dessus donne en résumé les grandes étapes de cette course : une succession de figures dont les aires sont de plus en plus petites. Au fur et à mesure de la progression, il est de plus en plus difficile de gagner de la place : chaque décimale gagnée coûte. L’observation de l’ensemble de ces figures semble montrer que l’on arrive à un palier qui laisse penser que l’aire minimale se situe aux alentours de 0,38 ou 0,39. Mais ceci n’est qu’une vague intuition issue de la considération de quelques figures et, de même que pour les origamis, seule une démonstration permettrait de valider définitivement cette intuition. Tant qu’il n’est pas étayé par une démonstration, le résultat pressenti peut s’avérer complètement faux... et c’est d’ailleurs ce qui arrive ici ! En 1928, soit onze ans après que Kakeya eut posé son problème, un mathématicien russe nommé Abram Besicovitch obtenait un résultat totalement déconcertant :
Théorème de Besicovitch. – Il est possible de retourner une aiguille dans une aire aussi petite que l’on veut !
Ce résultat va au delà de tout ce que l’on pouvait espérer pour ce qui est de l’amenuisement de la figure, à tel point qu’il en devient difficile à croire. Que dit-il au juste ? Il signifie que si l’on se donne une aire, même toute petite –par exemple égale à 0,1– alors il existe une figure dans laquelle l’aiguille peut se retourner et dont l’aire vaut 0,1 ; de même pour 0,01, pour 0,001, etc. Au bilan, l’aire envisagée, si minuscule soit-elle, est celle d’une figure où le retournement a lieu.
Les aiguilles parallèles
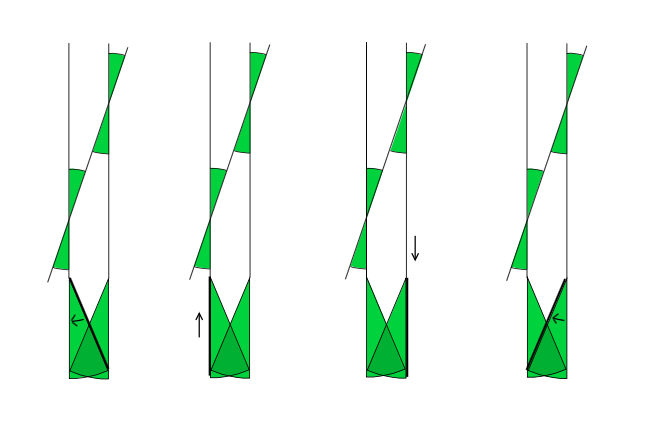
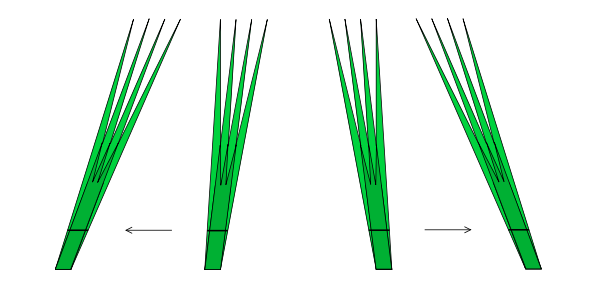
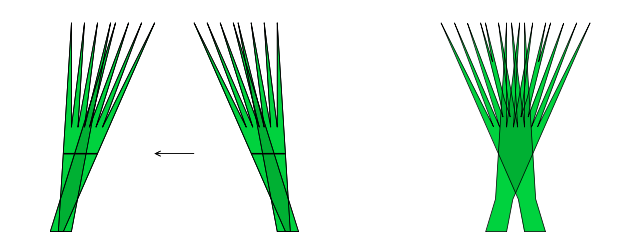
Il semble complètement paradoxal qu’il soit possible de déplacer une aiguille dans une aire aussi petite que l’on veut. Pour mieux comprendre ce phénomène déroutant, on va le mettre en évidence dans une variante bien plus élémentaire du problème de Kakeya : celle des aiguilles parallèles. On prend cette fois comme situation de départ deux aiguilles placées parallèlement et on se demande simplement comment passer de l’une à l’autre en couvrant le moins d’espace possible. La première solution qui vient à l’esprit prend la forme d’un parallélogramme : il s’agit d’un simple glissement de l’aiguille que l’on maintient bien parallèle tout au long du mouve- ment. Ce déplacement est représenté à gauche dans l’illustration ci-dessous. Dans le cas très particulier où les positions de départ et d’arrivée de l’aiguille se situent sur une même ligne, le déplacement de l’aiguille le long de cette ligne suffit à relier ces deux positions. L’aiguille consi- dérée étant idéale, c’est-à-dire sans épaisseur, celle-ci parcourt par conséquent un segment de droite et l’aire balayée est alors nulle. On ne peut bien sûr pas faire mieux, cette solution est donc optimale. En revanche, dans le cas général où les positions ne sont pas sur une même ligne, la solution du parallélogramme n’est pas la meilleure, il est en effet possible de déplacer l’aiguille de façon très économe en combinant judicieusement deux rotations.
La situation est très similaire à celle du théorème de Besicovitch : n’importe quelle quantité, même toute petite, correspond à l’aire d’une figure qui permet la translation de l’aiguille. Par conséquent, le problème de Kakeya pour les aiguilles parallèles n’a pas de solution, il n’existe pas de figure meilleure que toutes les autres. On se trouve confronté à la notion d’existence d’une solution ; en réalité lorsqu’on cherche à résoudre un problème, il y a deux questions qui se posent :
– Existe-t-il une (ou plusieurs) solution(s) ?
– Si oui, quelle est-elle (ou quelles sont-elles) ?
En général, on a tendance à oublier la première question et à s’attaquer directement à la
seconde. C’est exactement ce qui s’est passé dans ce livre, jusqu’à présent nous avons cherché une solution sans jamais douter de son existence. Pourtant rien n’était là pour garantir cette existence... Le théorème de Besicovitch vient nous ramener à la réalité : le problème de Kakeya n’a pas de solution puisqu’il n’existe pas de figure plus petite que toutes les autres dans laquelle l’aiguille puisse se retourner.
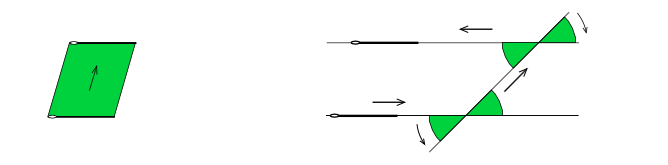

La construction de Besicovitch