Extrait du livre
La question de Kakeya
L’histoire de cette conjecture débute par une question si simple d’apparence que la réponse semble aller de soi. Mais les apparences sont trompeuses. Loin d’être évidente, cette question s’avère en réalité riche et profonde, et pour peu qu’on se laisse guider, son exploration conduit au cœur des mathématiques les plus modernes. Cette question « si simple » a été posée pour la première fois au début du XXe siècle par le mathématicien japonais Sôichi Kakeya :
Quelle est la plus petite surface à l’intérieur de laquelle il est possible de déplacer une aiguille de manière à la retourner complètement ?
De façon plus concrète, c’est comme si Kakeya, considérant une aiguille posée devant lui sur sa table de travail, se demandait comment dessiner la plus petite zone possible à l’intérieur de laquelle il pourrait faire glisser cette aiguille jusqu’à ce qu’elle se retrouve dans sa position initiale, la tête prenant la place de la pointe. La première réponse qui vient à l’esprit est le disque dont l’aiguille serait le diamètre et qu’une simple rotation suffirait alors à renverser complètement.
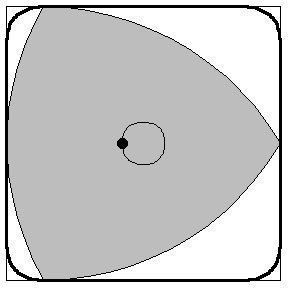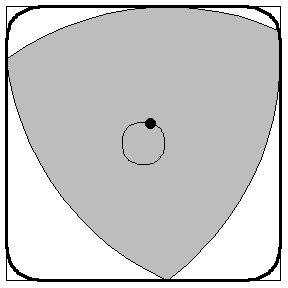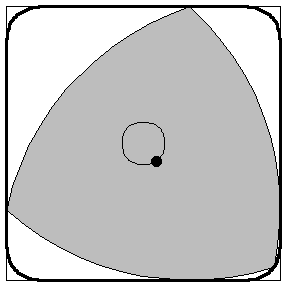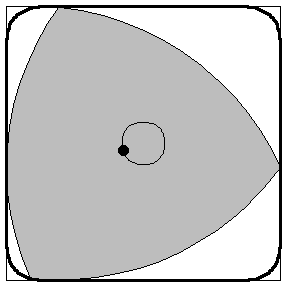
Aussi surprenant que cela puisse paraître, cette solution élégante et simple ne répond pas à la question de Kakeya : il existe d’autres façons de déplacer l’aiguille qui balaient de plus petites surfaces. Par exemple, au lieu de faire tourner l’aiguille autour de son centre, on lui fait effectuer des rotations successives autour de ses extrémités. Une figure se dessine alors d’elle-même : le triangle de Reuleaux.
Un calcul rigoureux de l’aire de cette figure montre qu’elle est plus petite que celle du disque (ce calcul est proposé dans l’encart coloré de la page suivante). Ainsi la figure que l’on pressent naturellement – le disque – n’est pas la solution au problème de Kakeya. Il se trouve que le Reuleaux ne l’est pas davantage, on peut en effet retourner une aiguille dans un triangle équilatéral dont l’aire est plus petite que celle du Reuleaux. Les dessins ci-dessous donnent l’idée du mouvement de l’aiguille à l’intérieur d’un tel triangle.
La question de Kakeya
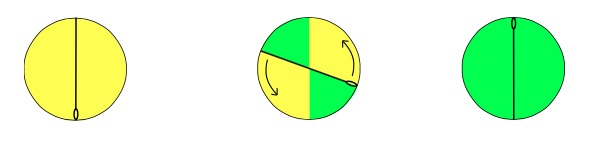
- Calculer l'aire d'un disque de diamètre 1.
Le triangle de Reuleaux

- Calculer l'aire d'un triangle de Reuleaux dessiné avec des arc de cercle de rayon 1.


Le triangle équilatéral

- Calculer l'aire d'un triangle équilatéral de hauteur 1.
Question ouverte
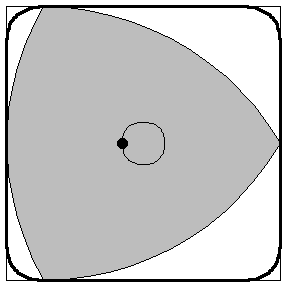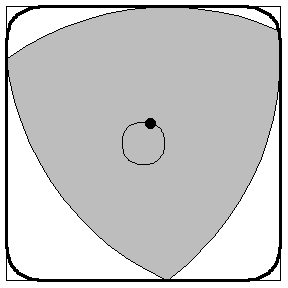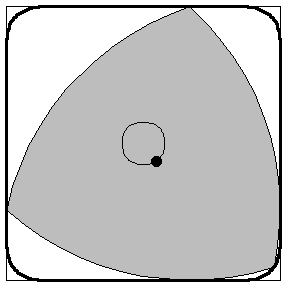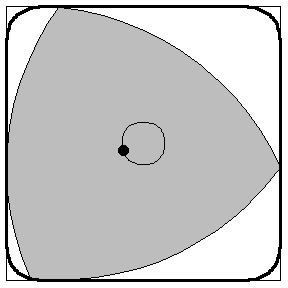
- Calculer l'aire de la surface occupée par le triangle de Reuleaux en mouvement ci-dessus.