Les équations différentielles
Extrait du livre
Les équations différentielles sont présentes dans tous les domaines de la science, elles régissent le mouvement des planètes, les lois de l’électricité, la dynamique des populations, etc. La première d’entre elles est apparue en même temps que le calcul différentiel avec Newton et Leibniz aux alentours des années 1700, elle a permis de déduire, à partir d’une loi fondamentale, les trajectoires des planètes autour du soleil. Plus encore, elle a montré que la connaissance à un instant donné de la position et de la vitesse de chaque planète suffit à prédire leur trajectoire ad vitam aeternam. Au XVIIIe siècle débute alors une période de foi absolue en l’idéal déterministe : il s’agit de traduire chaque phénomène naturel sous forme d’équations différentielles, lesquelles permettent ensuite, à partir d’une situation donnée, de décrire l’évolution dudit phénomène pour tous les temps futurs et passés.
Les équations différentielles sont par nature radicalement différentes de celles que l’on étudie dès les années de collège : les équations algébriques. Ces dernières font intervenir une inconnue symbolisée par la lettre x que l’on essaie de déterminer au moyen de calculs algébriques.
Par exemple l’équation 2x − 1 = 0 donne pour solution x = 1/2 .
Dans une équation différentielle, l’inconnue n’est plus un simple nombre mais une fonction tout entière que l’on symbolise par la lettre f . De plus, comme leur nom l’indique, ces équations font intervenir le calcul différentiel, c’est-à-dire le calcul de dérivées.
À titre purement illustratif, on peut citer l’équation différentielle 2f ′ − f = 0, qui signifie que l’on cherche une fonction f égale au double de sa dérivée.
La résolution de telles équations, c’est-à-dire la recherche de la fonction inconnue f , relève du savoir-faire du mathématicien. Bien sûr, toutes les équations différentielles ne sont pas de la même difficulté : si certaines, assez simples, relèvent de petites manipulations un peu similaires à celles que l’on effectue pour les équations algébriques, d’autres en revanche demeurent rétives à toutes formes de résolution.
Le problème de l'équerre
On va montrer au moyen d’une équation différen- tielle qu’un certain mouvement d’équerre engendre une parabole. Le mouvement est le suivant : on fait glisser l’angle droit de l’équerre sur une droite tout en astreignant un des côtés de l’équerre à coulisser sur un point fixe A. Les positions successives de l’autre côté de l’angle droit représentent une famille de droites qui dans leur ensemble forment une courbe qui semble être une parabole. Un raisonnement simple faisant intervenir une équation différentielle va en donner la confirmation.
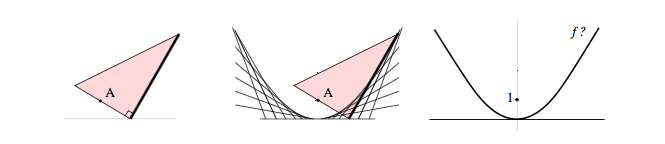
Contrairement à tous les problèmes qui se sont posés jusqu’à présent, ce n’est plus une simple valeur que l’on recherche mais bien une fonction f , celle dont la représentation graphique est justement la courbe enveloppe. Afin de déterminer cette fonction inconnue f , il est nécessaire de traduire en langage mathématique l’égalité des pentes au point de contact. Et puisque la pente d’une courbe est donnée par la fonction dérivée f ′, l’égalité des pentes se réduit donc à une égalité faisant intervenir la fonction f et sa dérivée f ′

